5分钟阅读
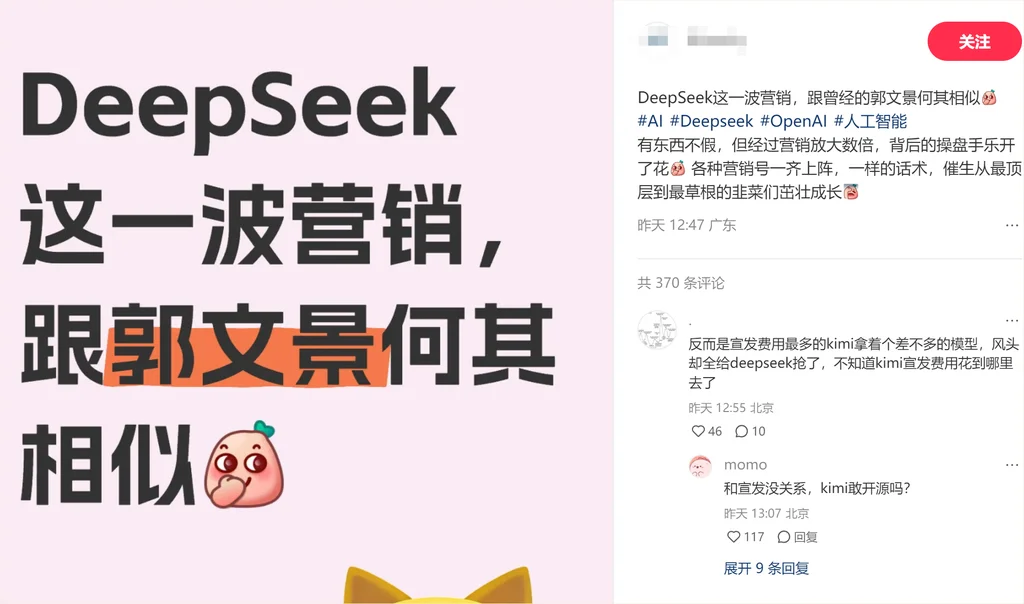
Deepseek R1应用数学可视化,果然数学是最美的!
前言
继续昨天的话题Deepseek R1 的应用。 其实,这么说吧,R1 能完成的工作,使用 openai 的 o1 也可以完成,只是 R1 的成本更低。 在上一篇文章中,我们就介绍了有位老哥做了个数学可视动画的(案例一),效果不错,读者也比较关注,接下来我们继续这个应用,并为大家实践一下。
题外话(很长的题外话🥱)
补充上篇的引用出处
上一篇文章中,有人留言,说我未著名出处。嗯🤔,确实小编的过错,已经紧急扣除、罚没了 0 元年终奖💢。
然而因为微信公众号的修改制度,再添加已经比较难了,这里为上一篇文章加上引用来源,均在老马的 X 上,各位可以自行找到出处:
- 视频来源:@CodeByPoonam
- 案例一:@christiancooper
- 案例二:@Sumanth_077
- 案例三:@itsPaulAi
- 案例四:@awnihannun
- 案例五:@rileybrown_ai
- 案例六:@alexocheema
- 案例七:@awnihannun
- 案例八:@nobody_qwert
- 案例九:@private_llm
- 案例十:@doesdatmaksense
- 案例十一:@reach_vb
- 案例十二:@akshay_pachaar
然而小编也是做了许多思考和努力的,一是验证来源的可靠性,并准备了实践行动,今天的文章解释进一步详细介绍和时间案例一“数学可视化的”,二是翻译和润色工作,让文章更加易懂,三是配图和视频,让文章可读性更高。翻译部分,一字一句翻译,虽然用了 AI 但还是要审核的,各位看官,作为一个小公众号,还请多抬贵手,如有纰漏敬请理解🙏🙏!
说到来源,此处值得深思
🤔 很好奇,当国内还在讨论,Deepseek 的所谓 营销能力 和 无用 时,国外的一众技术大佬和 AI 从业者,已经从实践中,验证 R1 的能力,已经讨论如何基于 Deepseek 团队公开的论文,进行复用和迭代!


对于普通的使用者来说,R 1 其顿悟和推理能力,如果只是聊聊天,很难用到,所以就有了不如其他 AI 模型的感觉,只有开发者和学术研究人员,需要用到其推理能力的,才会觉得 R 1 真的好!
另外国内的产品更多的重应用层,而有点忽略了底层算法研究(可能是大众的感受,或者是某些“大佬”的言论所致),在用户增长方面,又特别会“来事”(对,就是某 K、某 D,某 W,虽然产品很不错),但是铺天盖地的营销导致民众条件反射:“热点都是营销出来的😂“!反而一贯低调的 Deepseek,注重底层精进,给老外扎扎实实震撼到了!当然,还有 Qwen。
胡言乱语了,我是个旁观者,非 AI 技术的研发者,不懂算法,仅是一家之言🙏。
言归正传,以下回到 R 1 的超炫酷应用-数学可视化这个话题。
Math-To-Manim
作者介绍
Cooper 使用 R1 为他编写 Manim 程序,实现数学的可视化。他开源了该项目:https://github.com/HarleyCoops/Math-To-Manim
除了昨天给大家演示的勾股定律可视化,他还有个更加炫酷的量子电动力学 Quantum Electrodynamics 案例。
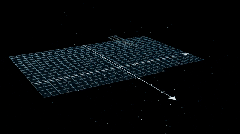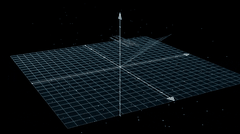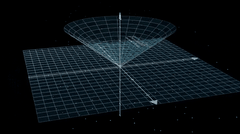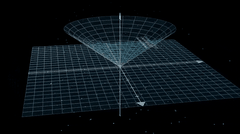
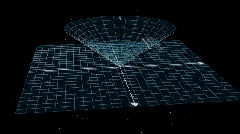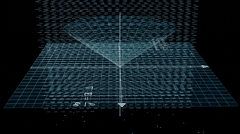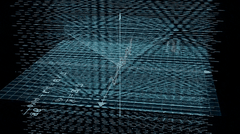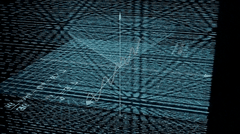


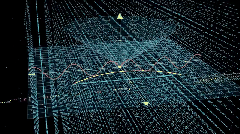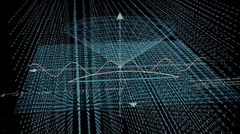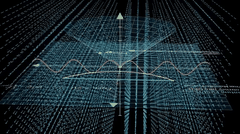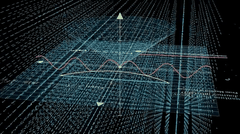
今天先根据作者的教程,我们跑一边。虽然我觉得,有些步骤是换个工具也可以,例如第一步,提示词和生成代码阶段,完全可以使用 cursor 得 ide 工具完成。
使用流程
安装
拉取项目
git clone https://github.com/HarleyCoops/DeepSeek-Manim-Animation-Generator
cd DeepSeek-Manim-Animation-Generator
设置环境
这里需要到 Deepseek 开发者平台 https://platform.deepseek.com 申请API。
# Create and configure .env file with your API key
echo "DEEPSEEK_API_KEY=your_key_here" > .env
# Install dependencies
pip install -r requirements.txt
安装 FFmpeg
-
- Windows:
- Download from https://www.gyan.dev/ffmpeg/builds/
- Add to PATH or use:
choco install ffmpeg
- Linux:
sudo apt-get install ffmpeg - macOS:
brew install ffmpeg
- Windows:
启动
python app.py
使用流程
输出 Manim 程序
先通过可视化界面,跟 R1 聊天。例如我先以 copper 给出的案例,稍微改了一下提示语:
# Role
You are a research and development expert, proficient in Python and Manim languages. Simultaneously possessing excellent artistic and visual skills, I can output executable Manim code according to my needs.
# Task
I will input rough requirements, you will understand and think about them, and ultimately output a Manim program that is perfect.
# Input
Begin by slowly fading in a panoramic star field backdrop to set a cosmic stage. As the camera orients itself to reveal a three-dimensional axis frame, introduce a large title reading ‘Quantum Field Theory: A Journey into the Electromagnetic Interaction,’ written in bold, glowing text at the center of the screen. The title shrinks and moves into the upper-left corner, making room for a rotating wireframe representation of 4D Minkowski spacetime—though rendered in 3D for clarity—complete with a light cone that stretches outward. While this wireframe slowly rotates, bring in color-coded equations of the relativistic metric, such as ds2=−c2dt2+dx2+dy2+dz2ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2, with each component highlighted in a different hue to emphasize the negative time component and positive spatial components. Next, zoom the camera into the wireframe’s origin to introduce the basic concept of a quantum field. Show a ghostly overlay of undulating plane waves in red and blue, symbolizing an electric field and a magnetic field respectively, oscillating perpendicularly in sync. Label these fields as E⃗\vec{E} and B⃗\vec{B}, placing them on perpendicular axes with small rotating arrows that illustrate their directions over time. Simultaneously, use a dynamic 3D arrow to demonstrate that the wave propagates along the z-axis. As the wave advances, display a short excerpt of Maxwell’s equations, morphing from their classical form in vector calculus notation to their elegant, relativistic compact form: ∂μFμν=μ0Jν\partial_\mu F^{\mu \nu} = \mu_0 J^\nu. Animate each transformation by dissolving and reassembling the symbols, underscoring the transition from standard form to four-vector notation. Then, shift the focus to the Lagrangian density for quantum electrodynamics (QED): LQED=ψˉ(iγμDμ−m)ψ−14FμνFμν.\mathcal{L}_{\text{QED}} = \bar{\psi}(i \gamma^\mu D_\mu - m)\psi - \tfrac{1}{4}F_{\mu\nu}F^{\mu\nu}. Project this equation onto a semi-transparent plane hovering in front of the wireframe spacetime, with each symbol color-coded: the Dirac spinor ψ\psi in orange, the covariant derivative DμD_\mu in green, the gamma matrices γμ\gamma^\mu in bright teal, and the field strength tensor FμνF_{\mu\nu} in gold. Let these terms gently pulse to indicate they are dynamic fields in spacetime, not just static quantities. While the Lagrangian is on screen, illustrate the gauge invariance by showing a quick animation where ψ\psi acquires a phase factor eiα(x)e^{i \alpha(x)}, while the gauge field transforms accordingly. Arrows and short textual callouts appear around the equation to explain how gauge invariance enforces charge conservation. Next, pan the camera over to a large black background to present a simplified Feynman diagram. Show two electron lines approaching from the left and right, exchanging a wavy photon line in the center. The electron lines are labeled e−e^- in bright blue, and the photon line is labeled γ\gamma in yellow. Subtitles and small pop-up text boxes narrate how this basic vertex encapsulates the electromagnetic interaction between charged fermions, highlighting that the photon is the force carrier. Then, animate the coupling constant α≈1137\alpha \approx \frac{1}{137} flashing above the diagram, gradually evolving from a numeric approximation to the symbolic form α=e24πϵ0ℏc\alpha = \frac{e^2}{4 \pi \epsilon_0 \hbar c}. Afterward, transition to a 2D graph that plots the running of the coupling constant α\alpha with respect to energy scale, using the renormalization group flow. As the graph materializes, a vertical axis labeled ‘Coupling Strength’ and a horizontal axis labeled ‘Energy Scale’ come into view, each sporting major tick marks and numerical values. The curve gently slopes upward, illustrating how α\alpha grows at higher energies, with dynamic markers along the curve to indicate different experimental data points. Meanwhile, short textual captions in the corners clarify that this phenomenon arises from virtual particle-antiparticle pairs contributing to vacuum polarization. In the final sequence, zoom back out to reveal a cohesive collage of all elements: the rotating spacetime grid, the undulating electromagnetic fields, the QED Lagrangian, and the Feynman diagram floating in the foreground. Fade in an overarching summary text reading ‘QED: Unifying Light and Matter Through Gauge Theory,’ emphasized by a halo effect. The camera then slowly pulls away, letting the cosmic background re-emerge until each component gracefully dissolves, ending on a single star field reminiscent of the opening shot. A concluding subtitle, ‘Finis,’ appears, marking the animation’s closure and prompting reflection on how fundamental quantum field theory is in describing our universe.
提示语部分,也可以通过 dify 等工具,建立一个工作流,用于生成准确的提示语。 如下,根据“勾股定理可视化”给出的提示词。
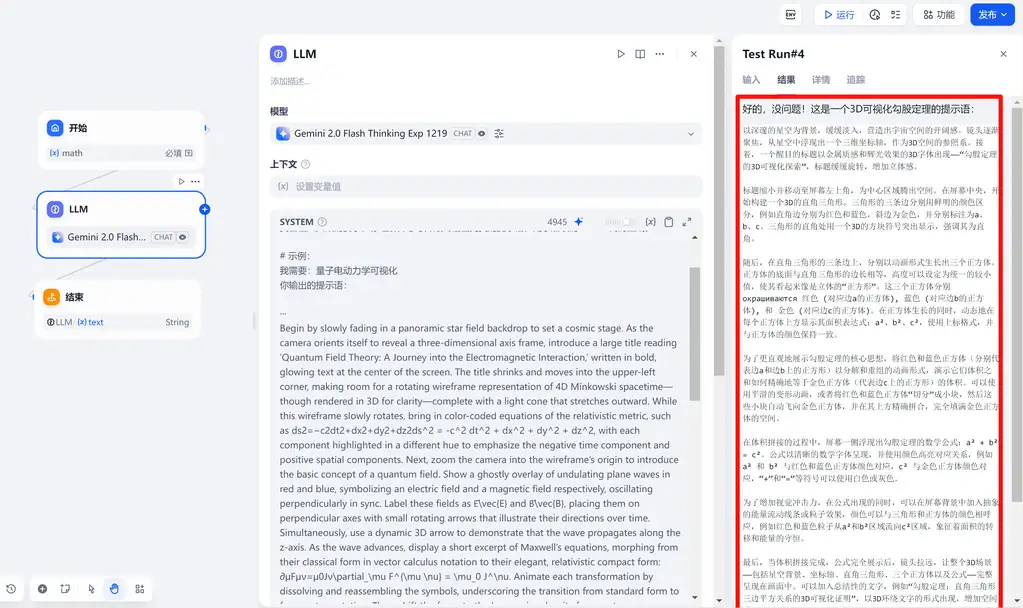
最后 R 1 的输出。
上面是使用作者的聊天界面完成的,过程运行代码会报错,需要修改。不知道作者是不是一次搞定的😂。
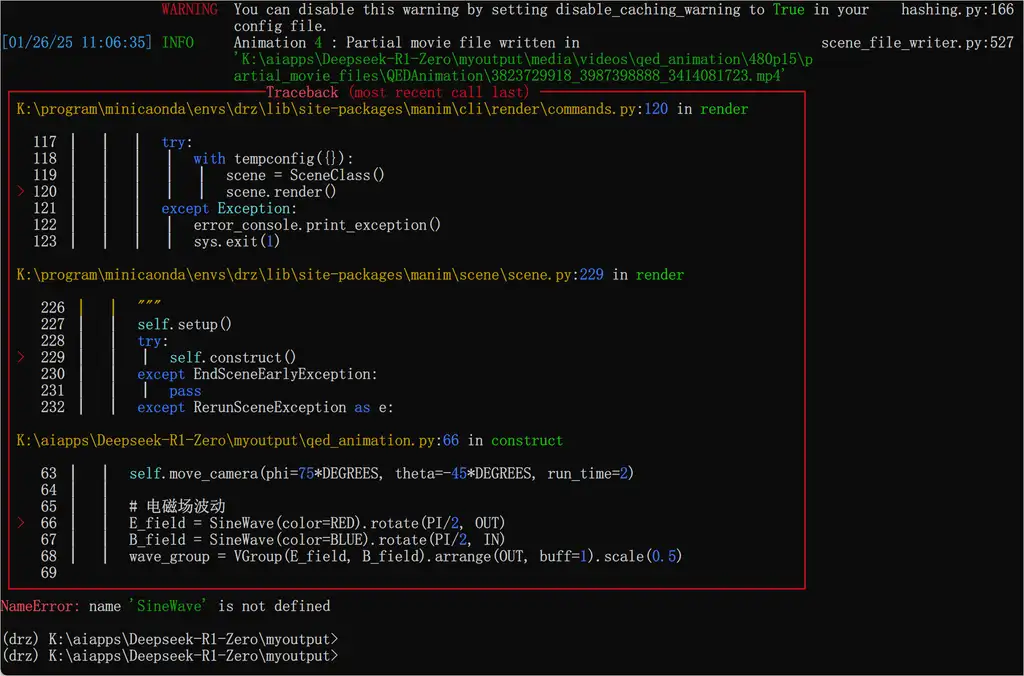
R1 返回了代码:
from manim import *
import numpy as np
config.background_color = BLACK
config.frame_rate = 30
config.pixel_height = 720
config.pixel_width = 1280
class QEDVisualizationFinal(ThreeDScene):
def construct(self):
# ========== 1. 宇宙开场 ==========
stars = VGroup(*[
Dot3D(
point=np.random.uniform(-7,7,3),
radius=0.008*np.random.random(),
color=WHITE,
).set_opacity(0.6 + 0.4*np.random.random())
for _ in range(400)
])
axes = ThreeDAxes(
x_range=[-6,6],
y_range=[-6,6],
z_range=[-4,4],
axis_config={"color": GREY}
)
title = Text("量子场论:电磁相互作用的旅程", font_size=36, font="Microsoft YaHei")
self.play(
LaggedStartMap(FadeIn, stars, lag_ratio=0.01, run_time=3),
Create(axes, run_time=2),
Write(title, run_time=2)
)
self.play(title.animate.scale(0.6).to_corner(UL))
self.wait(1)
# ========== 2. 时空结构 ==========
minkowski_grid = Surface(
lambda u, v: [u, v, 0],
u_range=[-6,6],
v_range=[-6,6],
resolution=(12,12),
color=TEAL
).set_opacity(0.2)
light_cone = Surface(
lambda u, v: [np.sqrt(u**2 + v**2), u, v],
u_range=[-3,3],
v_range=[-3,3],
resolution=(12,12),
color=YELLOW
).set_opacity(0.3)
metric_eq = MathTex(
r"ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2",
substrings_to_isolate=["-c^2 dt^2", "dx^2", "dy^2", "dz^2"]
).set_color_by_tex("-c^2 dt^2", RED).set_color_by_tex("dx^2", BLUE)\
.scale(0.8).to_corner(UR)
self.play(
FadeIn(minkowski_grid),
Create(light_cone),
Write(metric_eq),
run_time=3
)
self.begin_ambient_camera_rotation(rate=0.1)
self.wait(3)
# ========== 3. 电磁场 ==========
E_field = ParametricFunction(
lambda t: [t, np.sin(3*t), 0],
t_range=[-3,3],
color="#FF0000"
).rotate(PI/2, OUT)
B_field = ParametricFunction(
lambda t: [t, np.sin(3*t + PI/2), 0],
t_range=[-3,3],
color="#0000FF"
).rotate(PI/2, IN)
wave_group = VGroup(E_field, B_field).arrange(OUT, buff=1.5)
# 修正箭头动画问题
prop_arrow = Arrow3D(
start=ORIGIN,
end=2*OUT,
color="#FFD700",
resolution=5,
stroke_width=4
).set_opacity(0) # 初始不可见
self.play(
FadeOut(minkowski_grid),
FadeOut(light_cone),
Create(wave_group),
run_time=2
)
# 分步显示箭头
self.play(
prop_arrow.animate.set_opacity(1).shift(2*OUT),
run_time=2
)
self.wait(2)
# ========== 4. 麦克斯韦方程 ==========
maxwell_classic = VGroup(
MathTex(r"\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0}"),
MathTex(r"\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}")
).arrange(DOWN).to_edge(LEFT)
maxwell_rel = MathTex(
r"\partial_\mu F^{\mu\nu} = \mu_0 J^\nu"
).to_edge(RIGHT)
self.play(Write(maxwell_classic), run_time=2)
self.wait()
self.play(
TransformMatchingShapes(
maxwell_classic.copy(),
maxwell_rel,
path_arc=PI/2
),
run_time=3
)
self.wait(2)
# ========== 5. QED核心 ==========
lagrangian = (
MathTex(
r"\mathcal{L}_{\text{QED}} = \bar{\psi}(i \gamma^\mu D_\mu - m)\psi - \tfrac{1}{4}F_{\mu\nu}F^{\mu\nu}",
substrings_to_isolate=[r"\psi", r"D_\mu", r"\gamma^\mu", r"F_{\mu\nu}"]
)
.set_color_by_tex(r"\psi", "#FFA500")
.set_color_by_tex(r"D_\mu", "#00FF00")
.set_color_by_tex(r"\gamma^\mu", "#00FFFF")
.set_color_by_tex(r"F_{\mu\nu}", "#FFD700")
.scale(0.7)
.to_edge(UP)
)
self.play(
FadeOut(wave_group),
FadeOut(prop_arrow),
Write(lagrangian),
run_time=2
)
self.wait(2)
# ========== 6. 费曼图 ==========
feynman = VGroup(
Line(LEFT*2, ORIGIN, color="#0000FF", stroke_width=4),
Line(RIGHT*2, ORIGIN, color="#0000FF", stroke_width=4),
ArcBetweenPoints(ORIGIN, UP, angle=PI/2, color="#FFFF00", stroke_width=4)
)
self.play(Create(feynman), run_time=2)
self.wait(2)
# ========== 7. 终场 ==========
final_text = Text(
"QED:通过规范理论统一光与物质",
font_size=36,
font="Microsoft YaHei",
color="#87CEEB"
)
self.play(
FadeIn(final_text),
run_time=3
)
self.wait(3)
self.play(*[FadeOut(mob) for mob in self.mobjects])
self.play(Write(Text("终", font_size=72, font="Microsoft YaHei", color=WHITE)))
self.wait(2)
执行代码
保存文件
将代码保存到项目目录下,或者文件夹中,qft_visualization.py
运行代码
manim -pqh qft_visualization.py QuantumFieldVisualization
当然,为了加快速度,也可以给定预览参数:
manim -pql qft_visualization.py QuantumFieldVisualization --disable_caching --resolution=1280,720 --fps=30
等待完成
最终输出
输出的动画在 video 中。
最终结果,是没有作者的案例那么炫酷的,可能需要抽卡😂,但是视频把数学公式通过可视化方式展示出来了,普通人更加容易看懂,大功一件!
视频不完美,我只贴片段出来。后面研究透了,再放出来🥱。

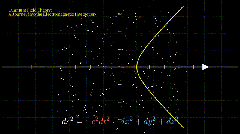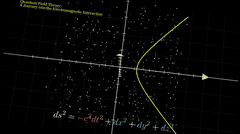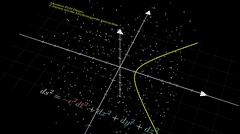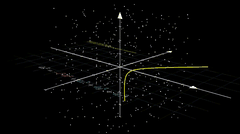
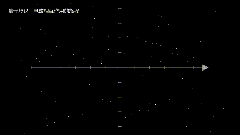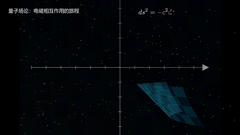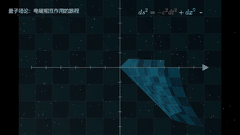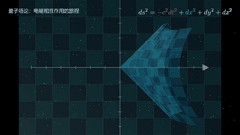
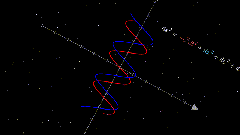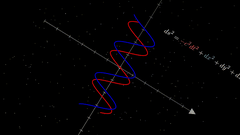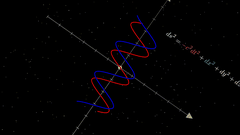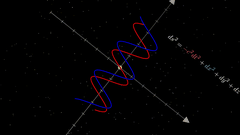

由于是预览画质,所以视频分辨率有点低,大家可以生成更高分辨率的试试。
更多测试案例
以下案例,我就直接用 gemini 帮我输出提示词了,我输入了数学公式名称。
勾股定理可视化

黄金比例

傅里叶变换可视化

分形公式-科赫雪花
用了 gemini 给我的提示词:
输出Manim python程序,创造一个令人惊叹的3D科赫雪花分形可视化动画。
**开场:**
1. **宇宙星空背景:** 从缓慢淡入的广阔星空背景开始,营造深邃的宇宙空间感。
2. **3D坐标轴**: 镜头缓缓移动,展现出一个精细的3D坐标轴框架,作为我们3D分形世界的基准。
3. **标题**: 在屏幕中心以闪耀的金属质感字体,逐渐显现标题:“三维科赫雪花:分形之美”。标题可以带有轻微的呼吸光效,增强视觉冲击力。
4. **标题归位**: 标题缩小并移动到屏幕左上角,为后续的雪花生成过程腾出中心区域。
**第一阶段:基础三角形的构建**
1. **初始三角形**: 在3D坐标轴的原点,从无到有地构建一个正三角形。三角形可以使用具有金属光泽的材质,例如金色或银色,并带有轻微的反射效果,使其更具立体感。
2. **三角形生长动画**: 三角形的边可以采用生长动画,从线段逐渐变成具有一定厚度的金属条,使其在3D空间中更具存在感。
**第二阶段:迭代生长过程 (3D化)**
1. **迭代过程可视化**: 将科赫雪花的二维迭代规则巧妙地转化为三维空间中的生长。
2. **突出边**: 在三角形的每一条边上,高亮显示中间三分之一的部分。
3. **3D凸起**: 从高亮部分,以垂直于三角形平面的方向,动态“生长”出一个小的正四面体(或者更简单的,一个等边三角形棱柱)。这个凸起过程要平滑且富有节奏感。
4. **替换与连接**: 原边中间三分之一的部分逐渐收缩消失,新生成的四面体(或棱柱)完美地连接到两侧的边段上,形成新的、更复杂的雪花轮廓。
5. **颜色迭代**: 为了清晰展示迭代层次,可以为每一层迭代赋予不同的颜色,例如第一层是金色,第二层是银色,第三层是青铜色,以此类推,或者使用更炫酷的渐变色方案。
6. **动态镜头**: 在迭代过程中,镜头可以轻微地缩放和旋转,始终聚焦在雪花的生长细节上,并保持整体结构的完整可见。
**第三阶段:细节与光影**
1. **材质与光照**: 随着迭代次数增加,雪花变得越来越复杂,材质可以逐渐调整为更细腻、更具有反射性的金属材质,例如抛光金属或水晶质感。
2. **动态光照**: 引入动态光照效果,例如环绕雪花旋转的光源,或者呼吸式的闪烁光点,使雪花的表面光影变幻,突出其3D结构和精细的纹理。
3. **阴影效果**: 在雪花下方添加一个微妙的阴影,投射到地面(例如XY平面),增强其悬浮在3D空间中的真实感。
**第四阶段:最终展示与炫酷特效**
1. **完整雪花**: 当雪花完成预设的迭代次数后,停止生长,展现一个完整而精美的3D科赫雪花分形。
2. **自旋转**: 让雪花开始缓慢地自旋转,全方位展示其复杂的3D结构和美丽的细节。
3. **色彩呼吸**: 雪花的颜色可以开始缓慢地呼吸式变化,例如在金色、蓝色、紫色等色调之间循环渐变,营造梦幻般的视觉效果。
4. **粒子特效**: 在雪花旋转的过程中,可以添加一些细微的粒子特效,例如环绕雪花飞舞的微小光点,或者从雪花边缘逸散出的光尘,增加画面的灵动性和科技感。
5. **背景互动**: 星空背景可以与雪花的色彩变化产生互动,例如当雪花变为蓝色时,背景星空也略微偏蓝,形成色彩呼应。
**结尾:**
1. **镜头拉远**: 镜头逐渐拉远,最终将完整的3D科赫雪花置于浩瀚的星空背景之中,形成强烈的视觉对比。
2. **总结文字**: 在屏幕下方淡入一行总结文字:“3D科赫雪花:数学之美与无限的想象”,或者更具诗意的语句。
3. **淡出**: 所有元素,包括雪花、坐标轴、文字和背景,都缓慢淡出,最终画面回归纯粹的星空,留下无限的遐想。
**风格**:
* **科技感与艺术感**: 整体风格兼具科技的精确性和艺术的唯美性。
* **金属质感**: 雪花主体材质可以以金属质感为主,突出其几何结构的硬朗和精确。
* **梦幻色彩**: 色彩运用可以大胆梦幻,例如金属色与渐变色的结合,营造出迷离而富有吸引力的视觉效果。
* **流畅动画**: 所有动画过程都力求平滑流畅,节奏舒缓,让观众沉浸在分形之美的探索之旅中。
请基于以上提示,创作Manim python代码,呈现一个震撼人心的3D科赫雪花分形可视化动画。






这就是神奇而迷人的数学! ❗️😮
写在最后
这个项目,如果将手动部分变得更加自动化,那么是可以作为教学的可视化工具,制作科普视频使用。有兴趣的大佬可以二开,也是是个赚钱的项目😎。
关注我公众号(设计小站):sjxz 00,获取更多 AI 辅助设计和设计灵感趋势。